Neural Networks and Deep Learning Models
Neural Networks
Deep learning (DL) is one aspect of the broader family of machine learning (ML) algorithms based on artificial neural networks (ANN)[1]. Deep learning and neural networks are unique in that they can be applied as supervised, semi-supervised, or unsupervised ML methods.
Neural networks are inspired by and modelled after biological systems of information processing which exist in nature. They are composed of layers of perceptrons which represent individual neurons existing as cellular pathways in the brains of organisms.
Neural networks however have various differences from biological brains. Specifically, they tend to be symbolic and static, relying more on information processing in a representational manner, whereas the biological brains of living organisms are malleable and analogue.
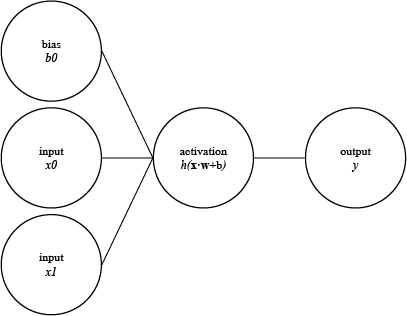
Figure 1. Perceptron
Perceptrons are structural units which compose a neural network. They take an input, have an assigned weight, receive a bias, and are designated an activation function. Learning is performed through mapping the input using weights and bias onto the output domain via the activation function.
Certain activation functions include:
- Sigmoid
- Tanh
- Softmax
- ReLU
- Leaky ReLU
- GLU
Neurons are arranged into layers, where the outputs of neurons in one layer form the inputs of neurons in the next layer. A network is therefore composed of multiple such layers of neurons. The number of neurons in each layer can be heterogeneous. These minimally include one input layer, one output layer, and at least one hidden layer (bridging the input and output layers).
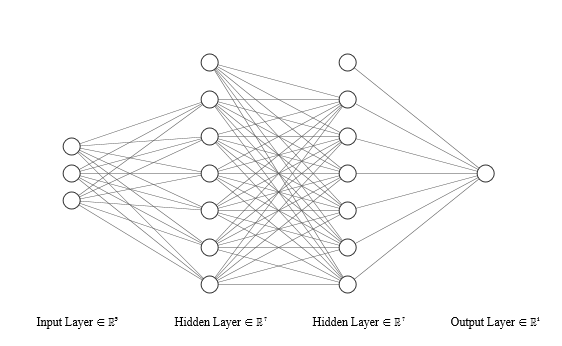
Figure 2. Neural Network
Through feed forward propagation, values of features are assigned to each input neuron and fed through the network with randomly initialized weights. The difference between the values of outputs of neurons in the output layer and the true and empirical values are then calculated, yielding us our errors.
Errors can be calculated in various ways, including:
- Mean Absolute Error (MAE)
- Mean Squared Error (MSE)
Commonly, the Mean Squared Error is employed as the Loss function, and is formulated as:
\[MSE = \frac{1}{n} \sum_{i=1}^{n}(y_i-\hat{y}_i)^2\]The errors are then propagated backwards through the network in the form of deltas, and stochastic gradient descent is used to update our weights. Once this cycle is repeated on all the data the network is being trained on over multiple epochs, we arrive at a set of weights which can then be used on new out-of-sample data for prediction.
Neural networks are highly inscrutable models with poor interpretability compared to, for example, linear regression where coefficients of features are directly interpretable. However, the beauty of neural networks lies in the robustness of their feature extraction capabilities which can elicit nuances and subtle patterns from data without direction.
Deep Learning
Deep learning is a special case of artificial neural networks, where the adjective ‘deep’ refers to the use of multiple hidden layers bridging the input and output layers of the network.
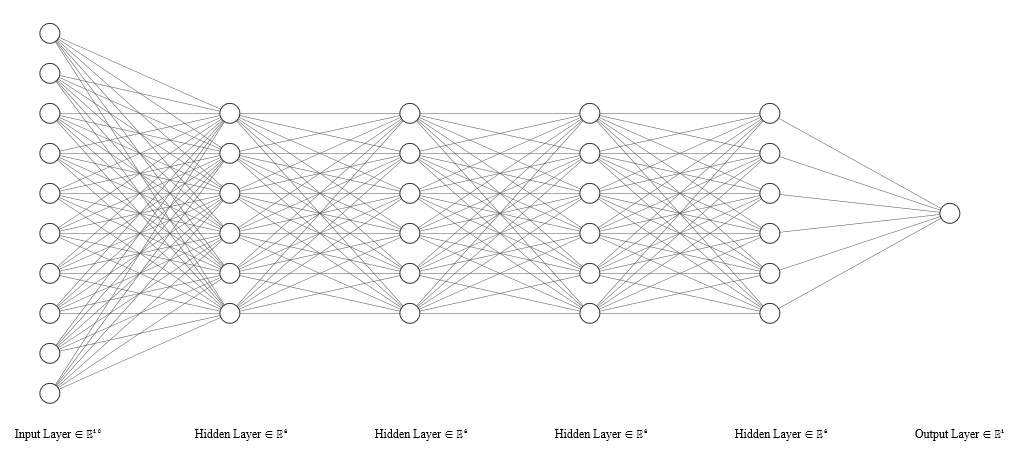
Figure 3. Deep Learning Neural Network
Ordinarily, a neural network without significant loss in generality or accuracy benefits by trading-off between complexity and time with just 2 hidden layers. Deep learning neural networks therefore trade-off the significant time it takes to train for the additional accuracy, nuance, and explanatory power the network gains in learning from the provided dataset.
Deep-learning architectures such as deep neural networks, deep belief networks, deep reinforcement learning, recurrent neural networks, and convolutional neural networks have been successfully applied in fields such as computer vision, image generation, automatic speech recognition, natural language processing, computer translation, and many other sophisticated applications. Results produced surpass the performance of human-designed expert systems.