Regression Analysis
Regression analysis is a reliable generalised linear modelling technique for identifying which variables have an impact on an indicator of interest being investigated, as performing a regression allows us to understand the relevance of contributing factors and the degree to which they have an influence (if any) and in what manner.
Linear Regression
Linear regression in statistics is the approach of linearly modelling an observed scalar response variable using one or more explanatory variables[1]. Generally, for robustness we restrict our modelling to the multiple linear regression case, where the outcome of a single target is predicted using multiple features in a ML application. Linear regression is a powerful tool heavily used in econometrics, statistics, and machine learning and is used in modelling data where the dependent variable is continuous.
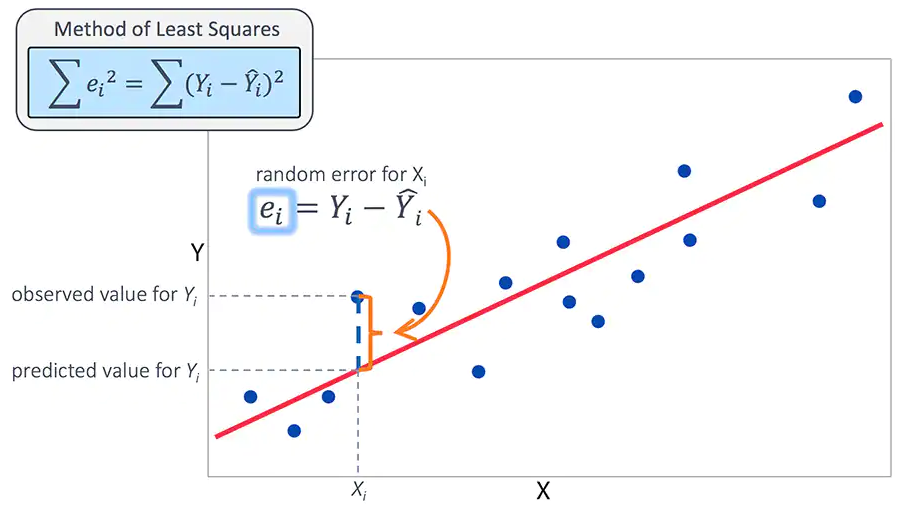
Figure 1. y = X * parameters + error
In a linear regression model, the target is represented by a continuous scalar variable which is observed and measured in our data. This data is usually of significant business interest and the goal of modelling our target is for prediction and forecasting. The target is linearly defined as the sum of the products of our observed features and their respective model parameter.
The difference in our prediction based on this linear function of features and model parameters and the target yields us an error. Optimisation algorithms such as Gradient Descent under statistical OLS assumptions allows us to choose model parameters which minimise the error. This gives us greater accuracy in predictions as the distance between our target and predictions is minimised. This is equivalent to finding a ‘line of best fit’ that closely maps onto our observed points as possible.
import numpy as np
import pandas as pd
df = pd.read_csv('./data.csv')
y = df.iloc[:, 0].values
X = df.iloc[:, 1:].values
# Ordinary Least Squares (OLS) under all OLS assumptions is Best Linear Unbiased Estimator (BLUE)
theta = np.linalg.inv(X.T @ X) @ (X.T @ y)
prediction = X @ theta
error = y - prediction
Different classes of regression models exist such as Ordinary Least Squares (OLS) regression, where the Mean Squared Error (MSE) is minimised.
Other forms of linear regression are available such as Generalised Least Squares (GLS) regression where the function of features and model parameters are specified in a different manner such as the use of a Generalised Method of Moments estimator.
Our unknown model parameters are estimated and learned from the observed dataset in this manner and can then be used on out-of-sample data to generate predictions by passing a predetermined set of features into the function.
Machine learning variants for multiple linear regression also exist, such as Ridge and Lasso regression which serve to regularise the disproportional impacts some features may have in determining our target by introducing a penalty into our linear function.